Probability Distribution Function of Momentum
Assuming that a time-invariant system in one dimension is completely described by a function in terms of x (psi of x), the Fourier transform, given by
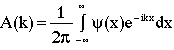 (1),
(1),
provides a way of expressing this information in terms of k. De Broglie's relation, given here in one dimension,
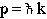 (2)
(2)
suggests a correlation between this and a function of momentum. From this, a function of k (phi of k), will be produced using the Fourier transform of psi. Taking a queue from the postulate relating the probability of finding a particle in space to the psi function, this function of k will be interpreted as one from which the probability density function of momentum can be constructed in an analogous way. Making use of the fact that integration of such a probability distribution function over all of k-space must generate a one, we expect a relation of the form
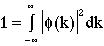 (3)
(3)
where the phi function embodies the information contained within A(k). Using the simplest possible correspondence between the A and phi functions, a constant, eta, is supplied to scale between them, yielding
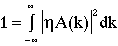 (4)
(4)
The task now is to determine this scaling factor, eta. This is begun by extracting this factor.
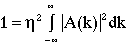 (5)
(5)
Introducing an alternate expression for the integrand gives
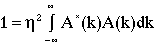 (6)
(6)
and substituting from eqn. 1 for A(k) yields
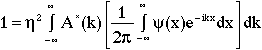 (7)
(7)
Rearranging
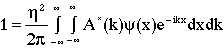 (8)
(8)
then changing the order of integration and removing psi gives
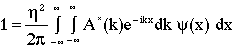 (9)
(9)
Identifying the inner integral as an inverse Fourier transform (although it is a bit obscured), we recognize that this corresponds to the conjugate of the psi function. The replacement is made.
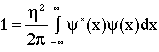 (10)
(10)
A required feature of the psi function is that the above integral be one. With this,
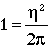 (11)
(11)
and algebra reveals
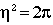 (12)
(12)
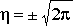 (13)
(13)
For convenience, eta will be chosen in the positive sense. Therefore, the function that we seek will behave as we wish, if given by
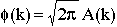 (14) (14) |
(1),
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)