Momentum Operator in x
The expectation value for momentum of a system in one dimension is given by
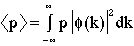 (1)
(1)
Application of the inverse Fourier transform allows the phi function of k to be represented in terms of x. This fact motivates us to explore to possibility of expressing the expectation value of momentum in these terms. Such an expression would be expected to take the form
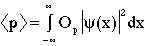 (2)
(2)
where Op represents something that extracts momentum information from the probability distribution function in positional form. To determine what Op represents, we begin by combining the two preceeding equations by their left sides, obtaining
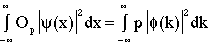 (3)
(3)
Substitution from De Broglie's relation, given here in one dimension,
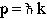 (4)
(4)
yields
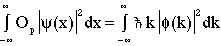 (5).
(5).
Introducing an alternate expression for magnitude squared of phi gives
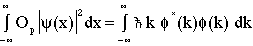 (6)
(6)
and substituting for phi and its conjugate in terms of the Fourier transform of psi, A(k), yields
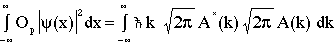 (7)
(7)
or
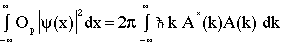 (8)
(8)
Replacing A*(k) with the transform of psi's conjugate that produces it, we have
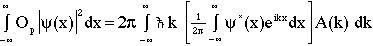 (9)
(9)
where A*(k) was targeted for replacement to ensure that the Op operator acts on psi and not its conjugate. Now, changing the order of integration and associated arranging gives
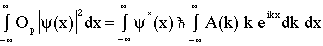 (10)
(10)
Noting that the inverse Fourier transform for psi is given by
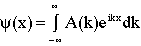 (11)
(11)
the inner integral of eqn. 10 is seen to differ only by a factor of k. This factor can be produced by differentiating the exponential once with respect to x, where the corresponding operator, independent of k, can be removed from the integral. This prompts the following line of reasoning.
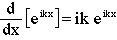 (12)
(12)
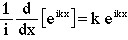 (13)
(13)
Making this replacement within the integral leads to
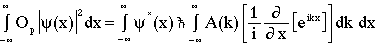 (14)
(14)
And, following the premeditated removal of the newly introduced terms, we have
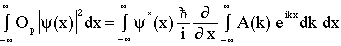 (15)
(15)
The inner integral is now the inverse Fourier transform representing psi, as shown in eqn. 11. It is replaced by psi.
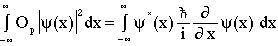 (16)
(16)
Next, rewriting psi and its conjugate as the magnitude squared of psi, we get
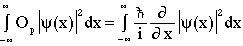 (17)
(17)
And comparing the two sides, we find the momentum operator in x to be
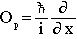 (18)
(18)
or, by bringing i into the numerator,
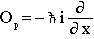 (19) (19) |
(1)
(2)
(3)
(4)
(5).
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)