Uniqueness of exp

The defining characteristic of the exp function states that

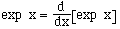(1)

Let's show that only one such function exists.
---
Say two such functions exist, labeled exp₁ and exp₂. The ratio between them is given

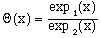(2)

Taking the derivative of both sides gives

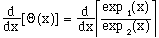(3)

Using the relation

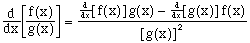(4)

yields

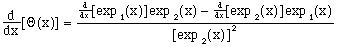(5)

By applying the defining relation of eqn. 1, we obtain

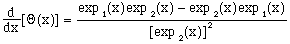(6)

And simplifying this, we get

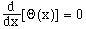(7)

Now, integrating both sides

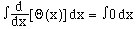(8)

produces

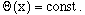(9)

from this into eqn. 2, we see

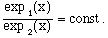(10)

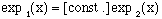(11)

Therefore, the functions exp₁ and exp₂ must be of the same form, as they are separated only by a constant. This suggests only one form satisfying the requirement of eqn. 1, thereby showing the uniqueness of the exp function.