Cofunction Identities
The cofunction identities
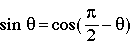 (19) (19) |
 (13) (13) |
are demonstrated by the following.
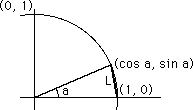
Fig. 1
|
Considering only the circumstances of the unit circle, as circles of other radii differ only by factors of r, we investigate a chord of length L, shown in Fig. 1, with an end point at (1,0). The other end point is given by (cos a, sin a), and its length is given by
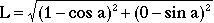 (1)
(1)
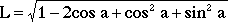 (2)
(2)
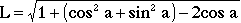 (3)
(3)
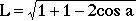 (4)
(4)
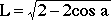 (5)
(5)
Placing a chord of the same length L into the same quadrant, with an end point at (0, 1),
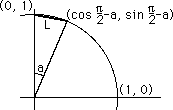
Fig. 2
this time L is given by
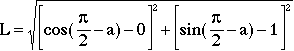 (6)
(6)
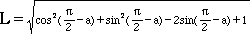 (7)
(7)
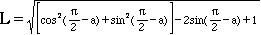 (8)
(8)
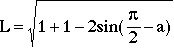 (9)
(9)
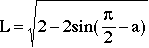 (10)
(10)
Equating by L,
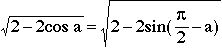 (11)
(11)
then
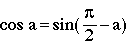 (12)
(12)
Although this was reasoned with the first quadrant in mind, there is nothing that binds the logic to that quadrant. Therefore, in general,
 (13)
(13)
Next, we start with this identity, rewritten as
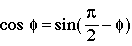 (14)
(14)
and assigning beta as
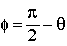 (15)
(15)
substitution provides
 (16)
(16)
 (17)
(17)
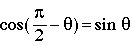 (18)
(18)
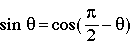 (19)
(19)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
(19)