Solutions to a quadratic equation
The x values of interest are those which satisfy the following equation:
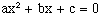 (1)
(1)
To find those values, the relationship must take a form where x is isolated and occurs only to the first power. Completing the square will fulfill the second requirement, so this will be the first step.
Start by making the x2 term's coefficient one:
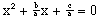 (2)
(2)
Thoughts on completing the square:
The purpose of completing the square is represented by the following, which equates a sum of zeroth, first and second terms to a perfect square.
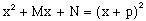 (3)
(3)
For this relationship to be satisfied, the following two conditions must be met:
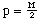 (4)
(4)
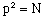 (5)
(5)
Combining, a relationship can be found for N in terms of M.
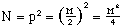 (6)
(6)
in this case:
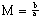 (7)
(7)
So, by the relationship found between M and N:
 (8)
(8)
For the sake of completing the square, introduce the corresponding expression for N:
 (9)
(9)
Without further ado, complete the square:
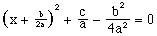 (10)
(10)
And algebra does the rest:
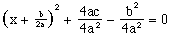 (11)
(11)
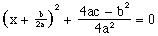 (12)
(12)
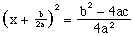 (13)
(13)
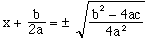 (14)
(14)
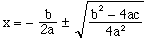 (15)
(15)
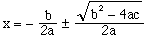 (16)
(16)
Finally, with this last step of simplification, the standard form of the quadratic formula emerges.
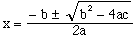 (17) (17) |
(1)
(2)
(3)
(4)
Combining, a relationship can be found for N in terms of M.(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)