The Fourier Transform
As it was purposed by Fourier, any well-behaved, periodic function, P(x), may be represented by
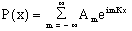 (1)
(1)
and from this, the coefficients represented by A can be expressed as
 (2)
(2)
Now the goal is to develop a transform of this type to apply to any well-behaved function, periodic or not. We begin with eqn. 1, where we use u as the argument.
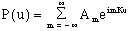 (3)
(3)
By substituting for the set of coefficients, Am, from eqn. 2, we obtain,
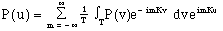 (4)
(4)
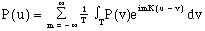 (5)
(5)
Making use of the relation
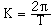 (6)
(6)
or
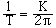 (7),
(7),
we substitute into eqn. 5, yielding
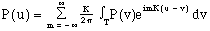 (8)
(8)
And rearranging gives
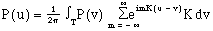 (9)
(9)
To accommodate all functions, including those which are not periodic, the period is taken to infinity. To reflect this new generality, the function being operated on will henceforth be denoted by f as opposed to the letter P, which was chosen to emphasize the requirement of periodicity.
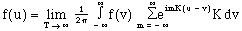 (10)
(10)
For a well-behaved function such as that which f is required to be,
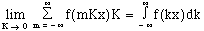 (11)
(11)
Because of the reciprocal relationship between T and K, as T goes to infinity, K goes to zero. Therefore, eqn. 11 may be applied here. This application to the appropriate part of eqn. 10 produces
 (12)
(12)
The focus now is to arrange this in such a way that a self-contained function of k emerges that completely describes the original function, f.
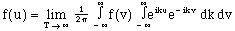 (13)
(13)
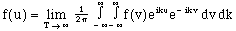 (14)
(14)
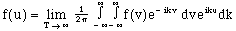 (15)
(15)
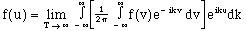 (16)
(16)
The interior grouped expression is a function of k containing the information represented by the original function f. This suggests that the expression behaves as we wish the transform to behave, so it can serve as the transform. Given in terms of x, we have
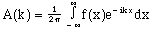 (17) (17) |
Also, the remaining outer operation provides a way of restoring f from this transform. It will therefore serve as the inverse transform, given in terms of x by
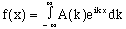 (18) (18) |
(1)
(2)
(3)
(4)
(5)
(6)
(7),
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)