The Fourier Series
As it was purposed by Fourier, any well-behaved, periodic function, f(x), may be represented by
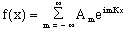 (1)
(1)
The goal here is to find the Fourier coefficients, represented by the subscripted terms of A. This will be accomplished by isolating these terms. Noting that integration of a complex exponential over an integral number of periods returns zero, and that an exponent of zero gives one suggests a strategy to proceed. We begin by multiplying both sides by a complex exponential chosen to expunge the factor of this type on the right hand side.
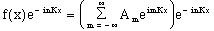 (2)
(2)
Distribution allows the factor to be brought into the summation.
 (3)
(3)
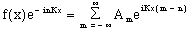 (4)
(4)
Now, we integrate over the fundamental period, over which all subperiods complete an integral number of cycles.
 (5)
(5)
Making use of the first noted fact that integration of a complex exponential over an integral number of periods returns zero, we recognize that in all cases where m and n are not equal, the result of the integration is zero.
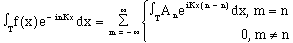 (6)
(6)
Now, considering the second noted fact that an exponent of zero gives one, we see that the exponential on the right is the multiplicative identity and can be removed.
 (7)
(7)
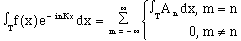 (8)
(8)
Performing the summation, where the only non-zero term is that of the upper condition, this simplifies to
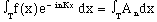 (9)
(9)
And doing this integration gives
 (10)
(10)
Finally, the A term is isolated by dividing both sides by the period, so
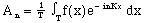 (11) (11) |
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)