Isolating Even Terms
Any function, f(x), that may be expressed by Taylor series expansion is represented by a series containing integer powers of x. Such powers of x with even exponents are called even terms, and those with odd exponents are called odd terms. Since all exponents are either even or odd, all terms must be one of the two. Grouping the even terms as feven and the odd as fodd gives,
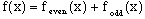 (1)
(1)
An operator to isolate even terms must have the effect of illiminating odd terms while preserving the even ones. To find such an operator, consider the property of odd terms:
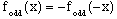 (2)
(2)
or
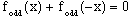 (3)
(3)
To remove these terms we might sum them to zero with this property by adding f(-x),
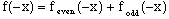 (4)
(4)
obtaining from eqns. 1 and 4:
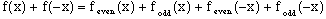 (5)
(5)
By eqn. 3, the odd terms cancel, leaving
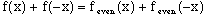 (6)
(6)
Now applying the property of even terms,
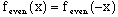 (7)
(7)
yields,
 (8)
(8)
or
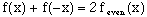 (9)
(9)
Finally, isolating the function's even terms gives:
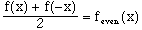 (10)
(10)
So, the operation to isolate even terms, called Ev[], is
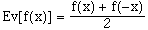 (11) (11) |
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)