Sinusoidal Derivatives
Sine's derivative is found first, starting by substituting
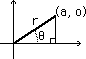
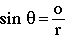 (1)
(1)
into the expression for sine's derivative.
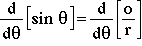 (2)
(2)
Next, theta will be replaced using
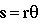 (3)
(3)
or isolating the angle
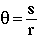 (4)
(4)
to produce
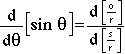 (5)
(5)
Since r remains constant over change in s, the 1/r terms may be extracted from the differential, giving
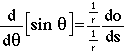 (6)
(6)
and this reduces to
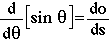 (7)
(7)
So, the derivative of sine is equal to do/ds. But, can this differential be expressed in terms of theta? Let's imagine the situation that the differential describes.
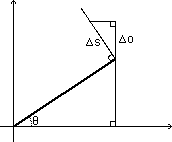
This diagram represents the situation of interest. The differential appears in the limit as delta s goes to zero, where the approximation of a line for the arclength becomes viable. Investigating the geometry
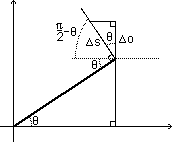
shows that this differential is the cosine of the angle theta.
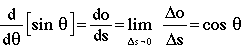 (8)
(8)
So,
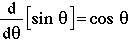 (9) (9) |
The derivative of cosine may be forged from this and the cofunction identities
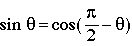 (10)
(10)
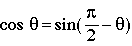 (11)
(11)
Using eqn. 11 to replace for the cosine function with sine, for which we already know the derivative, we get
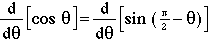 (12)
(12)
From eqn. 9,
 (13)
(13)
And, finally from eqn. 10,
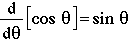 (14) (14) |
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(10)
(11)
(12)
(13)