Defining the delta function
A function, called the delta function and represented by
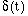 ,
,
is proposed to have the following properties:
1.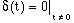 (i)
(i)
2. (ii)
(ii)
3.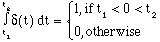 (iii)
(iii)
(Jackson 11)
How could such a function be represented?
---
Criterion iii with a negative lower limit of arbitrarily large magnitude suggests the running integral,
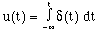 (1)
(1)
to appear as follows:
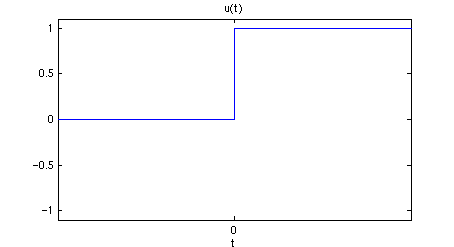
or in indefinate form
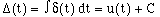 (2)
(2)
which with an appropriate vertical shift, absorbed by the arbitrary constant, C, gives delta prime:
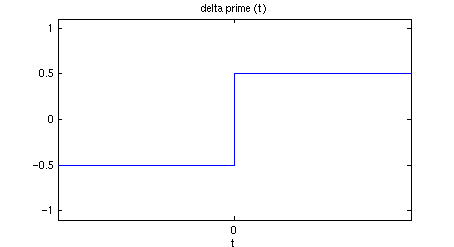
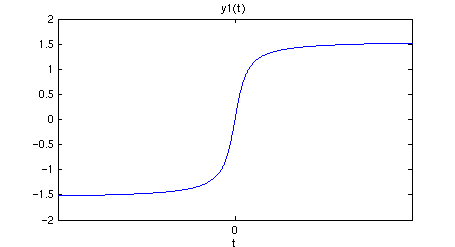
This is slightly reminiscent of the arctan function.
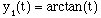 (3)
(3)
And even more so with a vertical scale,
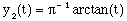 (4)
(4)
A horizontal scale, provided by multipling the arctan's argument by a number that approaches infinity, serves to imitate the steep feature of the integral.
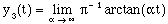 (5)
(5)
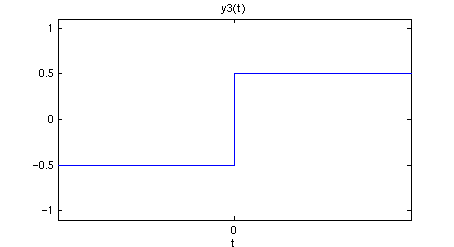
This same effect is produced by dividing the arctan's argument by a number that approaches zero.
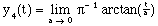 (6)
(6)
With the addition of an arbitrary constant,
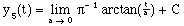 (7)
(7)
this replica function now shares all of the features expected of the indefinate form, given in eqn. 2 to be
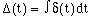 (8)
(8)
Therefore, the replica function should serve as the indefinate form.
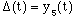 (9)
(9)
Manipulating this replica for use with the integral identity
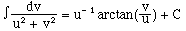 (10)
(10)
produces
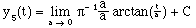 (11)
(11)
or
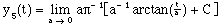 (12)
(12)
Substituting from the identity, eqn. 10, yields
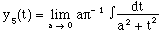 (13)
(13)
Now, finally applying eqn. 9
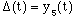 (9)
(9)
with eqn. 8
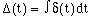 (8)
(8)
then
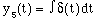 (14)
(14)
and that with eqn. 13 yields
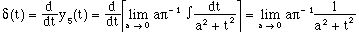 (15)
(15)
This relationship was developed from criterion iii. The relationship is also consistent with the other two criteria.
-
Criterion i is satisfied, as follows:
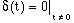 (i)
(i)
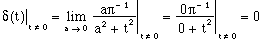 (t1)
(t1)
This verifies consistency with criterion i.
-
Criterion ii is satisfied, as follows:
 (ii)
(ii)
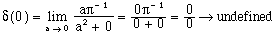 (t2)
(t2)
This operation is indeed undefined, verifying criterion ii.
-
So, it is suggested that the relationship
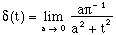 (16)
(16)
satisfies all defining properties of the delta function. Therefore,
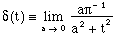 (17) (17) |
Jackson, Leland B. Signals, Systems, and Transforms
Addison Wesley, Reading, MA 1991
,
(i)
(ii)
(iii)
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(9)
(8)
(14)
(15)
(i)
(t1)
(ii)
(t2)
(16)